RL(Reinforcement Learning)에서 Agent는 Policy에 따라 어떤 Environment에서 특정 Action을 합니다. Action에 따라 State가 바뀌고, 바뀐 state에 따라 Reward를 받습니다.
따라서, RL은 가장 좋은 policy를 찾는 것이 목적이고, 가장 좋은 policy는 reward를 최대로 만듭니다.
Markov Chain
Markov Property
Markov Property는 확률 과정의 특수한 형태로서, 메모리를 가지고 있지 않다는 특성이 있습니다. 즉, Markov Property를 가진다면 현재 state는 바로 이전 state에만 영향을 받습니다.
다시 말해, 현재 state를 알면 미래 state를 추론할 수 있고, 미래의 state는 현재의 state만으로 결정된다고 정의합니다.

Markov Chain
Markov Chain은 Markov Property를 지닌 시스템의 시간에 따른 state 변화를 나타냅니다.
즉, 과거와 현재 state가 주어졌을 때, 미래 state의 조건부 확률 분포가 과거 state와는 독립적으로 현재 state에 의해서만 결정되는 environment를 말합니다.
이러한 state 공간이 discrete일 때 Markov Chain이라 하고, continuous일 때 Markov Process라 합니다.
- S : Set of Finite States
- P : State Transition Matrix

위 수식은 현재 state에서 다음 state로 이동할 조건부 확률을 나타냅니다.
State transition matrix는 모든 state에 대해 현재 state에서 다음 state로 이동할 확률을 나타내는 행렬입니다.
Markov Reward Process
MRP(Markov Reward Process)는 Markov Chain에 reward와 시간에 따른 보상의 감가율을 의미하는 γ(gamma)가 추가된 개념입니다.
Markov Chain에서는 state에 transition probability만 주어졌을 뿐, state transition이 얼마나 가치가 있는지는 알 수 없습니다. 하지만 MRP를 활용하면 state transition에 대한 value를 계산할 수 있습니다.
MRP의 구성 요소는 다음과 같습니다.
- S : Set of Finite State
- P : State Transition Matrix

- R : Reward Function
- State가 시간 t에서 s일 때, 시간 t+1에서 받을 수 있는 reward의 E(expectation).
- Expected Value : 각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값입니다.

- γ : 감가율
- 시간의 흐름에 따라 value를 얼마의 비율로 감가할지를 결정하는 비율.
- 0이면 미래의 reward를 전혀 고려하지 않고, 1이면 현재의 reward와 미래의 reward를 동일하게 평가한다.
- 주로 1보다 작은 값을 사용하지만, 항상 episode가 끝나는 경우에는 1을 사용하기도 한다.
- 1보다 작다면, 무한히 커지는 것을 방지하여 수치적으로 안정적이며, 수학적 분석이 쉬워진다.
- 먼 미래는 불확실하므로 감가를 적용한다.

MRP의 목적은 value를 계산하는 것입니다. 이것은 R을 사용하여 한 순간의 가치만을 계산하는 것이 아니라, 하나의 episode 혹은 전체 environment의 value를 한꺼번에 계산하는 것입니다.
- G : Return Value
- 현재 시점 t부터 전체 미래에 대한 감가된 reward의 합이다.
- 주로 전체 environment 보다는 episode 단위로 계산된다.
- 이 값을 통해 episode의 효율성이나 value를 판단한다.

G는 하나의 선택된 episode에 대한 R을 계산합니다, 따라서 P는 사용할 필요가 없습니다.
- V : State Value Function
- 현재 state에서 미래의 감가된 reward의 합의 E.
- G는 주로 episode 하나에 대한 value를 측정할 수 있지만, V로는 environment 전체에 대한 value를 측정할 수 있다.

위 수식을 s가 유한하고, R이 결정적이라고 가정하면 다음과 같은 형태로 바꿀 수 있습니다.

이것을 state value function bellman (expectation) equation이라고 합니다.
BEE(Bellman Expectation Equation)는 일반적으로 expectation을 Σ기호를 사용한 수열의 합으로 표현하며 현재 state와 다음 state의 관계로 나타냅니다.
또한, 다음과 같이 선형 연립방정식 형태로 표현할 수 있습니다.

BEE는 선형 방정식이기 때문에 직접해를 구하는 것이 가능합니다. 하지만, n이 커질수록 직접적으로 문제를 푸는 것이 어려워집니다.

Markov Decision Process
MDP(Markov Decision Process)는 MRP에 action과 policy가 추가된 확률 과정입니다.
MRP는 episode나 environment 전체의 value를 계산하는 것이 목적이고, MDP는 environment의 value를 극대화 하는 policy를 결정하는 것이 목적입니다.
- MRP : Agent는 시간의 흐름에 따라 state transition probability에 영향을 받는다.
- MDP : Agent는 시간별로 policy에 따라 action을 선택하고, state transition probability에 영향을 받는다.
MDP의 구성 요소는 다음과 같습니다.
- S : Set of Finite State
- P : State Transition Matrix
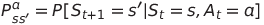
- R : Reward Function
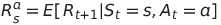
- γ : 감가율

- A : Set of Finite Action
- π : Policy Function
- Action을 선택할 확률.
- 즉, agent가 policy에 따라 action을 한다는 것은 확률이 높은 action을 할 가능성이 크다는 의미이다. 꼭 확률이 높은 action을 한다는 의미가 아니다.

MDP에서 agent의 action은 오로지 policy에 의해 결정되며 policy는 시간에 따라 변하지 않습니다.
Policy까지 고려했을 때의 P와 R은 다음과 같습니다.

- V : State Value Function
- 시간 t, state s에서 policy π를 따른다면 얻을 미래 value의 감가된 총합의 E.
- State를 중심으로 value를 평가.

- Q : State-Action Value Function
- 선택 가능한 action 중 하나를 수행했을 때의 value를 계산한다.
- 정책을 평가하기 위해 action을 중심으로 value를 평가.
시간 t, state s에서 a라응 action을 취한 후, policy π를 따른다면 얻을 미래 value의 감가된 총합의 E.

V와 Q의 관계는 다음과 같이 표현할 수 있습니다.

MDP에서 state가 변한다는 것은 P와 π의 영향을 동시에 받는다는 것과 같습니다.
따라서 action에 따른 policy와 state transition probability의 expectation을 구함으로써 policy를 고려한 P를 구할 수 있습니다.

위 식을 간략화하면 다음과 같습니다.

MDP에서 policy를 평가하는 것은 state value fundtion을 구하는 것과 같습니다.
MDP에서 state value function의 의미는 어떤 policy를 따랐을 때 reward의 총 합계를 구하는 것입니다.
MDP Optimal Value Function
Optimal value function은 optimal state value function과 optimal action value function으로 나눌 수 있습니다.

MDP에서 optimal action value function을 안다는 것은 가장 효율적인 action을 선택할 수 있는 policy를 안다는 것과 같습니다.
따라서 optimal action value function을 찾아낼 수 있다면 MDP 문제를 해결할 수 있습니다.

Optimal value를 얻도록 action하게 만드는 policy가 바로 optimal policy(π*)입니다.

BOE(Bellman Optimality Equation)는 다음과 같이 정리할 수 있습니다.
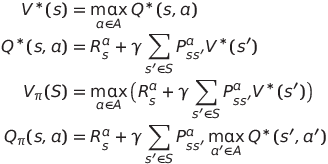
BOE는 선형방정식이 아니므로 일반해가 존재하지 않습니다.
하지만, 반복적 알고리즘을 통해 해를 계산할 수 있습니다. (예: policy evaluation, policy iteration, value iteration, Q-learning, SARSA)
'AI' 카테고리의 다른 글
| Windsurf IDE, Claude Code 사용하여 웹 개발하기 (1) | 2025.08.18 |
|---|---|
| [RL] Overview (1) | 2021.05.22 |
| [DL] Save and Load model on Keras (2) | 2021.04.05 |
| [DL] SimpleRNN with Keras (0) | 2020.12.05 |
| [DL] Image Classification using ResNet with CIFAR-10 Dataset on Keras (0) | 2020.11.15 |

댓글